ENERGIE ELECTRIQUE: Machine synchrone

Principes généraux

La machine synchrone se compose d'une partie tournante, le rotor, et d'une partie fixe, le stator. Le rotor peut se composer d'aimants permanents ou être constitué d'un bobinage alimenté en courant continu et d'un circuit magnétique (électro-aimant).
Pour produire du courant, on utilise une force extérieure pour faire tourner le rotor : son champ magnétique, en tournant, induit un courant électrique alternatif dans les bobines du stator. La vitesse de ce champ tournant est appelée « vitesse de synchronisme ».
Il n'est pas possible de faire démarrer correctement, sans aide extérieure, une machine synchrone en connectant ses enroulements statoriques directement sur un réseau alternatif.
Si l'on n'entraine pas le rotor par une force extérieure, il est possible de la faire tourner en alimentant ses enroulements statoriques par un courant alternatif dont la fréquence augmente progressivement de zéro à la fréquence de synchronisme et en faisant en sorte que la tension aux bornes des enroulements soit proportionnelle à la fréquence. Sa vitesse de synchronisme sera directement liée à la fréquence de l'alimentation électrique.
Un autre moyen est de réaliser l'auto-pilotage de la machine, c'est-à-dire de maintenir l'orthogonalité du flux magnétique rotorique par rapport au flux statorique⁵, par exemple, en disposant sur son axe un capteur qui délivre une information de la position du rotor. Cette information est traitée par un convertisseur électronique qui fournit le courant statorique à la machine, en phase avec sa force contre-électromotrice⁵.

Machine synchrone triphasée

Mise en équation

Méthode utilisée

Notations

Toutes les grandeurs statoriques sont repérées soit par l'indice _S soit par des indices en majuscules.
Toutes les grandeurs rotoriques sont repérées soit par l'indice _r soit par des indices en minuscules.

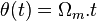L'angle $\theta (t) = \Omega_m .t \,$ correspond au décalage angulaire entre le stator et le rotor.

$L_S ; L_r \,$ : Inductances propres d'un enroulement du stator ; d'un enroulement du rotor.
$M_S \,$ : Inductance mutuelle entre deux enroulements du stator.
$M_{rS} \,$ : Valeur maximale de l'inductance mutuelle entre l'enroulement du rotor et un du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 ).

Hypothèse

La mise en équation n'est opérable que pour une machine à pôles lisses et dont le circuit magnétique est non saturé. Pour les autres machines, on apportera des correctifs permettant (avec plus ou moins d'exactitude) la prise en compte de leurs complexités.
Pour la suite on considère une machine pour laquelle :

Son circuit magnétique est homogène (entrefer constant) et non saturé. De ce fait, les diverses inductances sont constantes (entrefer constant).
Les courants des trois phases statoriques ont la même valeur efficace I_S (la machine est assimilable à un récepteur triphasé parfaitement équilibré).
Elle possède une seule paire de pôles (machine bipolaire). Les machines multipolaires se ramènent à une machine bipolaire au prix d'une transformation angulaire.

Les courants

Au stator

On fixe l'origine des temps de manière à pouvoir écrire :

$i_A (t) = I_S \sqrt{2} \cdot \cos \alpha_S \,$

On en déduit les courants des deux autres phases du stator :

$i_B (t) = I_S \sqrt{2} \cdot \cos \left(\alpha_S - \frac{2 \pi}{3}\right) \,$

$i_C (t) = I_S \sqrt{2} \cdot \cos \left(\alpha_S + \frac{2 \pi}{3}\right) \,$

Avec : $\alpha_S = \omega_S \cdot t \,$ , et $\omega_S \,$ : pulsation des courants statoriques.

Au rotor

Au rotor, il n'y a que le courant continu I_r alimentant la bobine du rotor par l'intermédiaire d'un contact glissant sur deux bagues collectrices.
Il n'y a pas de glissement dans le cas d'un moteur synchrone, seulement un léger angle de déphasage.
Remarque

Si le rotor est constitué d'un aimant, on considèrera une bobine produisant un moment magnétique équivalent, c’est-à-dire traversée par un courant I_r que l'on détermine à l'aide de la méthode d'Hopkinson (application du théorème d'Ampère à un circuit magnétique).

C’est-à-dire :

$L_a \,$ la longueur de l'aimant

$S_a ; S_b \,$ respectivement la section moyenne de l'aimant et celle de la bobine

On pose :

$\mathcal{M}_b = \mathcal{M}_a \,$

$NI_r .S_b= H.L_a.S_a \,$

En supposant que la bobine et l'aimant ont la même section, on obtient :

$NI_r = \frac{B_r.L_a}{\mu_0} \,$

Les flux

Flux à travers un enroulement statorique

$\Phi_A = L_S i_A + M_S i_B + M_S i_C + M_{rS} \cos \theta \cdot I_r ,$

Comme :

$i_A + i_B + i_C = 0 \,$ , alors $M_S i_B +M_S i_C = - M_S i_A \,$ ,

$\Phi_A = (L_S - M_S) i_A + M_{rS} \cos \theta \cdot I_r ,$

On pose

$(L_S - M_S) = \mathcal{L}_S \,$ : inductance cyclique

L'expression du flux devient alors

$\Phi_A = \mathcal{L}_S i_A + M_{rS} \cos \theta I_r \,$

l'expression du nombre complexe représentant le flux est

$\underline \Phi_A = \mathcal{L}_S \underline i_A + M_{rS} \underline I_r \,$

avec $\underline I_r \,$ la représentation complexe d'un courant sinusoïdal « fictif » de valeur maximale $I_r \,$ et de pulsation $\theta = \omega t \,$ .
En toute rigueur, cette substitution n'est valable qu'en régime établi : aucune modification de la charge ou de l'alimentation. C'est une condition nécessaire pour affirmer que la fréquence de rotation est exactement égale à la fréquence de l'alimentation.

Flux à travers un enroulement rotorique

Le flux traversant le rotor est le résultat de deux champ magnétiques :

Le champ tournant, créé par les enroulements statoriques ;
Le champ propre, créé par l'enroulement rotorique qui est constant (courant continu) mais qui tourne mécaniquement à la même vitesse que le précédent (machine synchrone). Avec la même limite qu'au paragraphe précédent : aucune modification de la charge ou de l'alimentation.

Les tensions

Tension aux bornes d'une phase du stator

$\ V_A = R_S . I_A + \frac{d\Phi_A}{dt} \,$

$\underline V_A = (R_S + j \omega_S \mathcal{L}_S) \underline I_A + j \omega_S \mathcal{M}_{rS} \underline I_r \,$

On pose $E_{av}$ la tension à vide, c’est-à-dire la tension lorsque $\underline I_A = 0$ (tension créée par le seul champ rotorique)

$\underline V_A = (R_S + j \omega_S \mathcal{L}_S) \underline I_A + \underline E_{av} \,$

Modélisation

Il existe plusieurs modèles équivalents de la machine synchrone suivant le nombre de paramètres dont on veut tenir compte.

Le modèle équivalent de Behn-Eschenburg

Le modèle de Behn Eschenburg ne s'applique que si la machine est non saturée et à pôles lisses. C'est le plus simple, il ne tient compte d'aucune saturation ni variation de l'entrefer. Il consiste à remplacer chaque phase de la machine par un ensemble de trois dipôles en série tels que la tension aux bornes de ce dipôle est égale à :

$\underline E_{av} = (R_S + j \omega_S \mathcal{L}_S) \underline I_A + \underline V_A = (R_S + j X_S) \underline I_A + \underline V_A \,$

avec :

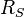$R_S \,$ et $X_S \,$ constants et indépendants du fonctionnement de la machine.

$\underline E_{av} = k \omega I_r \,$ uniquement proportionnelle à la fréquence de rotation et au courant d'excitation (courant rotorique).

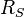Ce modèle convient bien aux gros turboalternateurs de forte puissance. On peut encore simplifier le modèle (et les calculs qui en découlent) en négligeant $R_S \,$ devant $X_S \,$ .

Le modèle équivalent de Potier

Détermination des paramètres du triangle de Potier.

Ce modèle est plus complet que celui de Behn-Eschenburg. Il tient compte de la saturation en faisant varier le courant d'excitation en fonction du courant traversant les bobines du stator. Cette modification du courant excitateur fait varier la fcem.
Dans ce modèle on a :

$i_r = i_{rv} - \alpha.I \,$

$E = V + R.I + j.\omega.\lambda.I \,$

Le modèle de Blondel à deux réluctances

Il permet de prendre en compte les variations angulaires de réluctance des machines synchrones à pôles saillants.

Stabilité statique

Article connexe : Stabilité des générateurs électriques synchrones.

La stabilité en régime dynamique du réseau électrique est son aptitude à éviter tout régime oscillatoire divergent et à revenir à un état stable acceptable. Ceci inclut l’intervention éventuelle des protections et automatismes divers fonction des perturbations envisagées⁶.

Schéma électrique équivalent d'un générateur synchrone.

La puissance active délivrée par une machine synchrone à ses bornes est égale à :

$P_{active} = U_{bornes}*I*\cos{\phi} = \frac{E \cdot U_{bornes}}{X_{generateur}} \cdot \sin{\delta}$

Avec les notations du schéma ci-contre, c'est-à-dire E la tension électromotrice du générateur, $X_{generateur}$ son impédance, I le courant, $U_{bornes}$ la tension à ses bornes, $\phi$ le déphasage entre courant et tension et $\delta$ l'angle interne du générateur, autrement dit l'angle entre U_bornes et E.

Deux angles internes sont possible quand la puissance délivrée par le générateur est égale à la puissance mécanique qui lui est fournie.

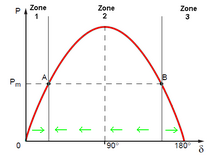
Les flèches en vert indique la direction que prend l'angle interne dans les différentes zones. On voit clairement que le point A est stable, le point B ne l'est pas⁷

Ce générateur reçoit une puissance mécanique, typiquement d'une turbine, notée Pm. À l'équilibre, la puissance entrante, mécanique, est égale à la puissance sortance, électrique. On néglige ici les pertes⁶. Pour cet équilibre deux angles internes sont possibles (cf. image).
L'angle interne du générateur est régi par l'équation suivante⁶ :

$\frac{J \cdot \omega_m}{p} \cdot \frac{d^2 \delta}{dt^2} = P_m - P_e$

Où $\omega_m$ est la vitesse mécanique du rotor, J le moment d'inertie du rotor, p le nombre de pôle du générateur et Pe la puissance électrique. D'après cette équation si la puissance mécanique est supérieure à la puissance électrique consommée, alors l'angle interne augmente et inversement. On en déduit le diagramme ci-contre quant à la direction que prend l'angle interne en cas de petite variation autour du point d'équilibre.

Notes et références

↑ Les quadrants II ou IV du plan couple-vitesse (dit des « des quatre quadrants »), figurant dans l'article « Quadrant (mathématiques) », avec la vitesse en ordonnée et le couple en abscisse. Comme toutes les machines électriques — qui sont par nature réversibles —, une machine synchrone passe sans discontinuité du fonctionnement « moteur » au fonctionnement « générateur » par simple inversion du signe du couple (charge entrainée ou entrainante, par exemple pendant les phases d'accélération ou de freinage) ou du signe de la vitesse (inversion du sens de rotation).
↑ BTS Électrotechnique (deuxième année) – Machine à courant continu – Quadrants de fonctionnement [archive], site physique.vije.net, consulté le 8 août 2012.
↑ Dans les quadrants I ou III du plan couple-vitesse définit dans la note ci-dessus.
↑ Description d'un moteur synchrone [archive], sur le site sitelec.org, 7 septembre 2001, consulté le 28 mars 2012.
↑ ^{a et b} P(en) P. Zimmermann, « Electronically Commutated D.C. Feed Drives for Machines Tools », Robert Bosch GmbH – Geschäftsbereich Industrieaurüstung, Erbach, Germany, p. 69-86 in Proceding of PCI Motorcon, septembre 1982, p. 78-81.
↑ ^{a, b et c} Stabilité dynamique des réseaux électriques industriels [archive]. Consulté le 18 décembre 2012 [PDF].
↑ Diagramme inspiré du polycopié Grundlagen der Hochspannungs- und Energieübertragungstechnik de la TU Munich, p. 246.

ENERGIE ELECTRIQUE

lundi 18 mars 2013

Machine synchrone